The target is to develop a tool, that converts sequential program text into data dependency graph. The language source code has to be written on is ANSI ISO C. With  this implementation it is supposed to investigate abilities and perspectives of a fully automatical approach to creation of  parallel programs. The resulting graph can be used as an independent form the machine arcitecture way of program representation.

Text analysis is spent in assumption of static memory distribution. Program couldn't hava dynamical memory allocation, e. g. malloc system call. Surely, statical analysis can't fully consider all C programming language features because of variety of functional features and widely used programming techniques, which programmers apply in their daily practice. For instance, it is very difficult to use statical analysis if pointer type and operations with objects of such a type which are stipulated in C language are included in representation. Therefore, this and similiar features are not analized in current version of developed analizer, and program end its work with diagnostical message when detects it. Existance check for not currently supported feature in C program is made at informational dependencies definition stage, after text recognition.

Main strategy of building graph using C program is strtegy of maximal separating of operations for getting widest representation of graph. In other words, it is maximization of number of independent among themselves operations. Arithmetical equations are converted in tree structure, on which basical number of operations and special transformations are implemented. For instance, it is possible to calculate the result of equation if values of variables which in this equation are are defined, linearize and simplify indexed expression and so on. Next, this structure is used in representation of information about dependencies. It can be noticed that there is no any analysis of parallel execution abitity for expressions, because changing of calculation flow may lead into incorrect or errorneous results (arithmetical floating-point operations are not commutative). But rearranging of calculations in expression is possible. It can be reached by preliminary calculating of functions with subsequent replacement of call with result. Note that such a function hasn't have any collateral effects.

Set of global variables if defined for each function, which operates with it. Weight of function, which determines its calculation comprehensiveness, is calculated. In theory, it is possible to make insertion of body of function with its actual parameters in call position. In С++ such a functions are marked with inline keyword. Unfortunately, this feature isn't implemented in current version. Several significant restrictions are applied on these functions. In our case the most significant restriction is unique return in function. This operator set so called control dependency and can't be interpreted in terms of informational dependencies directly. Unique (unconditional) return operator can be replaced with assigment of return value to a variable. If function body contains conditional operators with return, text can't be inserted in call position of function. Such a style of programming is widely used because of its convience and presentation.

Let's consider, how data dependency graph for block of C-program operators is being built. Following information is determined for each operator in block: set of input operators, set of output operators, weight of operator. This data is called operator context. Weight of operator is non-negative number, which defines calculation complexity of operator expressed, for example, in number of abstract machine times. Name, type, sign of entering in conditional operator and, if it is array variable, list of ranges which determine used part of array by each dimension with description of dimension of encountered in operator variable are set for input and output parameters.

Beacause body of each function should be inserted in call position, name of each variable in function is changed to unique one for whole program. This conversion consist of doubling number of undercores and adding of _number suffix where number is a number of block of C language operators, where variable name is declared. Numbering of blocks is through whole program and begins from zero. Suffix isn't used for global variables, this fact allows distinguishing globa names from other program names.

Block operator analysis is characterized by prezence of local variables, which scope is limited only by block where these variables are declared. Although overlapping of variable names of variables which defined in current and parent blocks (or globally) can occur, so distinguishing of different mentioning of the same name is needed. These problems are solved by the metod mentioned above.

Block operator contains list of local variables declarations and list of operators.

Блочный оператор состоит из списка деклараций локальных переменных и списка операторов. Для каждого блочного оператора порождается новый контекст, в котором регистрируются локальные переменные. Контекст объемлющего блока становится его родителем. Далее происходит анализ последовательности операторов блочного оператора на основе нового контекста. Входные и выходные параметры блока определяются как объединение входных и выходных параметров всех внутренних операторов. После проведения операции объединения контекстов внутренних операторов для описания внешних зависимостей из построенного объединённого контекста удаляются упоминания о локальных переменных блочного оператора. Результат такого просеивания будет входом/выходом для блочного оператора вцелом. В дальнейшем при анализе зависимостей в родительском блоке по отношению к переменным внутреннего блока будет использоваться только построенный таким образом контекст.

Зависимости для внешних переменных, использующих внутренние переменные блока, строятся следующим образом. Скалярные переменные и массивы сначала исключаются из списков входных и выходных зависимостей, затем анализируются индексы, и если они содержат вхождения локальных переменных (не важно, массивов или скаляров), то индексы заменяются на диапазон, описывающий длину соответствующего этому индексу измерения. Если элементы массива из диапазона входят в условные операторы, то такие диапазоны помечаются. Так поступают, поскольку невозможно гарантировать изменение всех элементов массива, соответствующих данному диапазону, и нельзя указать точно, какой элемент меняется.

Далее обратимся к методу анализа зависимостей в циклах. В виду сложности анализа производится только анализ цикла for при наложении на него следующих условий:

1. границы цикла должны быть заданы константными выражениями

2. индексные переменные должны меняться только в заголовке цикла строго с шагом единица и не должны меняться внутри тела цикла

3. Внутри тела цикла не должно быть операторов break/continue/return

Первое условие связано со сложностью анализа преобразований переменных вообще. Второе и третье условия гарантируют, что индекс пробежит все значения из диапазона определённого границами цикла. Игнорирование этих требований может привести к некорректному результату. Например, какой-то элемент массива из диапазона может остаться неинициализированным, но будет помечен как получивший новое значение. Последующие операторы будут думать, что значение этого элемента они должны получить от этого цикла, но в действительности они получат «мусор», а не то значение, какое бы получили при последовательном исполнении. Логика исходной программы будет нарушена. При этом требование единичного шага итерации цикла не критично и легко может быть снято, в текущей реализации присутствует из соображений простоты реализации.

Анализ зависимостей по данным в цикле разбивается на несколько этапов. На первом этапе для каждой итерации цикла производится анализ зависимостей переменных, встречающихся в теле цикла, от других итераций данного цикла. На следующем этапе производится преобразование зависимостей для тела тела цикла в зависимости от внешних по отношению к циклу переменных. Далее определяется выход цикла, то есть та часть данных, которая была изменена во время исполнения цикла. Далее во всех операторах, где будет использоваться переменные, которые использовались циклом, будут присутствовать в зависимостях только рассматриваемая изменяемая часть цикла. Например для цикла

выход будет a[1][2], a[2][3] … a[10][11], а не a[1][2], a[2][2], a[1][3] …

Анализ условных операторов (if, switch) производится следующим образом. Для построения зависимостей строится объединение In и Out от всех ветвей условного оператора. К сожалению, в статике редко удаётся предсказать, какая именно ветка условного оператора выполнится. Поэтому, затем, при преобразовании зависимостей в граф, весь условный оператор представляется как одна вершина.

Далее, по всем найденным зависимостям строится граф. Просмотр начинается с функции main С-программы, в которой производится проход по всем операторам функции. Если среди операторов встречается вызов функции или цикл, или условный оператор, то по ним принимается решение о том, нужно ли рассматривать данный оператор как единое целое, или можно его разделить на части и каждую часть рассматривать отдельно. Операция такого разбития оператора на составные части в дальнейшем будет называться операцией раскрытия оператора. В результате операции раскрытия вместо одной вершины соответствующей оператору получается группа вершин, состоящая из операторов, входящих в раскрываемый оператор.

Последовательность операторов, которые следуют естественным порядком, тоесть когда операторы выполняются строго последовательно один за другим, без операторов, в которых есть операторы переходов, будем называть линейным участком.

Таким образом, построение графа зависимости производится рекурсивно по всем составным операторам, которые преобразуются либо в одну вершину графа, если оператор не допускает операцию раскрытия, либо в множество вершин, если операция раскрытия допустима. Процесс добавления очередной вершины в граф состоит из определения типа зависимости от других вершин для данной вершины и определения того, какие данные необходимо передать между вершинами в случае наличия между ними зависимости. В случае обнаружения прямой зависимости по данным между двумя вершинами проводится ребро, для которого указываются переменные, участвующие в зависимости и объём пересылаемых данных. Если Out(i) и In(j) пересекаются, то создаётся ребро, направленное от i-ой вершины к j-ой. В случае обнаружения обратной зависимости между 2-мя операторами вершины аналогично соединяются ребром, но поскольку в данном случае важен только порядок следования операторов, а данные не имеют значения, то строится ребро с весом 0. В этом случае ребро направлено таким образом, чтобы не нарушать порядок следования операторов. Тем самым декларируется важность самого факта инициализации передачи данных, а что именно будет передано по ребру не имеет значения.

С целью оптимизации все дуги между парой вершин, независимо от их типа, объединяются в одну дугу с конкатенацией данных. Такой подход позволяет передавать требуемые данные в за одну операцию передачи данных, позволяя тем самым снизить расход времени связанный с латентностью коммуникационной среды.

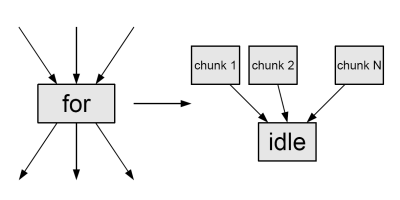
На начальном этапе производится раскрытие всех составных операторов до состояния, когда получаются либо атомарные, либо нераскрываемые операторы. Раскрытие различных составных операторов производится по-разному. Блочный оператор раскрывается всегда. Раскрытие цикла происходит только в том случае, если удается определить границы изменения итератора и в теле отсутствует передача управления (return/break/continue). При выполнении этих условий цикл преобразуется в последовательность итераций, где для каждой итерации явно прописывается значение индекса цикла. Иллюстрацией к раскрытию итераций цикла for является пример, приведённый на рисунке. К сожалению, в текущей реализации нет возможности раскрытия циклов while и do while, главным образом из-за сложности определения границ цикла и отсутствия итератора цикла. Не производится разделение на ветки операторов switch и if else.

Применительно к вложенным циклам можно сказать, что после раскрытия всех итераций получается огромное количество вершин, так, для простого алгоритма перемножения матриц (3 вложенных цикла) и матрицы 10х10 получается порядка 1100 вершин.

В приведённом примере видно, что раскрытие только верхнего цикла дает максимальную степень параллельности 10, тогда как раскрытие еще 2-го цикла увеличивает эту цифру в 10 раз. При таком подходе, т.е. раскрытии всех итераций необходима дополнительная процедура «свертки» графа в соответствии с реальным числом процессоров и минимизацией пересылок, что, к сожалению, в текущий момент не реализовано.

Рассмотрим способ построения фрагмента графа для линейного участка. Пусть S₁, S₂, …, S_i, …, S_N — последовательность операторов линейного участка. Между двумя операторами S_i и S_j, i<j имеется зависимость во всех случаях, если результаты исполнения i-го оператора нужны j-ому оператору. В данной ситуации, казалось бы, два данных оператора необходимо соединить ребром, однако, если между этими операторами присутствует оператор S_k, который модифицирует переменную, которая требуется на вход j-ому оператору, то будет проведено не одно ребро, а 2 ребра между вершинами, соответствующими операторам S_i, S_k и S_k, S_j.

Процесс построения начинается от последнего оператора и продолжается в обратную сторону. Для оператора, у которого переменная var ∈ In(i) входит во множество входов оператора, ищется ближайший к нему оператор, у которого данная переменная входит во множество выходов оператора var ∈ Out(i). Весом ребра становится количество байт, занимаемое переменной, участвующей в зависимости. Так продолжается до тех пор, пока не будет достигнут первый оператор. В случае, если для пары операторов прямая зависимость не выявлена, ищется обратная зависимость. Вне зависимости от наличия прямой или обратной зависимости для последовательности операторов ищутся зависимости по выходам.

Каждой вершине графа сопоставлен её вес. Как уже говорилось ранее, это число, характеризующее вычислительную сложность вершины. В данном случае это оператор, как атомарный, так и составной (цикл, условный оператор, вызов функции). Данная информация необходима в дальнейшем для алгоритмов планирования вычислений. В данной реализации вес оператора считается как число эталонных операций и в качестве эталонной операции выбрана операция сложения двух чисел с плавающей точкой. Таким образом, для атомарных операций можно произвести очень приблизительный подсчёт их времён исполнения относительно вычисления операции сложения. Для составных операторов всё обстоит несколько сложнее, поскольку они состоят из множества операторов. Среди множества операторов могут встречаться вызовы функций, о времени вычисления которых на этапе статического анализа программы может не оказаться сведений.

Для условных операторов вес вычисляется как сумма весов условия оператора и максимального значения веса одной из альтернатив. Вес линейного участка кода вычисляется как сумма весов составляющих его операторов.

Обратимся к вычислению весов циклов. Для определения веса цикла for необходимо знать численные значения границ изменений параметра цикла и вес его тела. Для нескольких вложенных операторов for:

вес будет вычисляться по формуле:

Weight =	U1	(… +	U2(I1)	(… +	Uk(I1, I2, …, Ik–1)	BodyWeight(I1, I2, …, Ik) + …) + …)
	Σ		Σ		Σ
	I1=L1		I2=L2(I1)		Ik=Lk(I1, I2, …, Ik–1)

где тело и диапазоны изменения границ вложенного цикла зависят от параметров объемлющих циклов. Как видно из приведённой формулы, большая степень вложенности влечёт большие вычислительные затраты при вычислении веса.

К сожалению, про число итераций цикла while как правило ничего сказать нельзя, поэтому вес цикла считается как вес его тела. Тоже самое относится и к циклу do while.

Project admin: Alexey Salnikov