|
Краткая информация
| Имя файла |
parser |
| Краткое описание |
По С-программе строит граф зависимостей по данным |
| Формат вызова |
parser {filename1}, ... {filenameN} |
Анализатор зависимостей по данным в C-программе
Целью является разработка программного средства, преобразующего текст последовательной программы в граф зависимостей по данным. В качестве языка выбран язык C (стандарт ANSI ISO). С помощью полученной реализации предполагается исследовать возможности и перспективы, связанные с применением полностью автоматического подхода к созданию параллельных программ. Построенный граф может использоваться как независимый от архитектуры машины способ представления программы.
Анализ текстов проводится в предположении статического распределения памяти. В программе не должно быть динамического выделения памяти, например системного вызова malloc. Конечно, при статическом анализе невозможно полностью учесть всех особенностей языка программирования C из-за разнообразия функциональных возможностей и широко применяемых программистами приемов программирования в своей повседневной практике. Например, очень сложно проводить статический анализ, если включить в представление тип данных указатель и операции над объектами этого типа, предусмотренные в языке C. Поэтому в текущей версии разработанного анализатора эта и подобные ей особенности языка не анализируются, и при их обнаружении программа прекращает свою работу выдачей диагностического сообщения. Проверка на наличие в C-программе не поддерживаемых в текущий момент особенностей проводится на этапе определения информационных зависимостей, который происходит после распознавания текста.
Основной стратегией при построении графа по C-программе является стратегия максимального разделения операций с целью получения наиболее широкого представления графа. То есть максимизации количества независимых между собой операций. Арифметические выражения переводятся в древовидную структуру, над которой реализован базовый набор операций и специальные преобразования. Например, можно вычислить значение выражения, если значения переменных в нем присутствующих определены, преобразовать в линейную форму и упростить индексное выражение и др. Далее эта же структура используется в представлении информации о зависимостях. Стоит заметить, что при работе не происходит анализа выражений на распараллеливаемость, поскольку изменение последовательности вычислений может привести к некорректным или «неправильным» результатам (обычные арифметические операции для чисел с плавающей запятой не коммутативны). Однако перераспределение вычислений в выражении возможно. Это может быть достигнуто путем предварительного вычисления результатов используемых функций, с последующей подстановкой результата в место вызова. Заметим, что такая функция не должна иметь побочных эффектов.
Для каждой функции определяется набор глобальных переменных, с которыми она оперирует. Определяется вес функции, характеризующий её вычислительную сложность. В теории, возможно сделать подстановку тела функции в место вызова, с подстановкой актуальных параметров. В С++ такие функции помечаются ключевым словом inline. К сожалению, в текущей реализации такая возможность не реализована. На такие функции накладывается некоторые существенные ограничения. В нашем случае самым серьезным ограничением является требование единственности оператора return у функции. Совершенно ясно, что оператор return задает так называемую зависимость по управлению, и на прямую не выразим в терминах информационных зависимостей. Единственный (безусловный) return может быть заменен на присвоение некоторой переменной возвращаемого значения. Если тело функции содержит условные операторы с return, в качестве выполняемого действия, то такой текст нельзя подставлять в место вызова данной функции. Подобный стиль написания функций довольно широко распространен в силу своих удобства и наглядности.
Обратимся к тому, как происходит построение дерева зависимостей для блока операторов C-программы. Для каждого оператора в блоке определяется следующая информация: множество входных параметров, множество выходных параметров, вес оператора. В дальнейшем, данная информация будет называться контекстом оператора. Вес — неотрицательное число, характеризующее вычислительную сложность оператора, выраженное, например, в количестве тактов абстрактной машины. Для входных и выходных параметров оператора указываются имя встречающейся в операторе переменной, тип переменной, признак вхождения переменной в условный оператор и, если это переменная-массив, список диапазонов - интервалов, определяющих используемую часть массива по каждому измерению, с описанием размерностей.
Поскольку в идеале для каждой функции программы происходит разворачивание её структуры с подстановкой в место вызова, то для каждой переменной, указанной в блоке, происходит преобразование её имени с целью получения уникального имени переменной для программы целиком. Всякое имя переменной в программе получается следующим образом: удваивается количество подчеркиваний, и к нему добавляется суффикс _число, где число - номер блока операторов языка C, в котором объявлено имя переменной. Нумерация блоков сквозная и начинается с нуля. Для глобальных имен суффикс не используется, это позволяет при чтении легко отличить глобальные имена от остальных имен программы.
Анализ блочного оператора характеризуется наличием локальных переменных, использующихся только внутри этого оператора, и невидимых другим операторам программы, расположенным на верхних уровнях. Кроме того, возможно перекрытие имен переменных, объявленных ранее в объемлющих блоках или глобально, поэтому следует отличать различные упоминания одного итого же имени. Данные проблемы решаются описанным ранее способом.
Блочный оператор состоит из списка деклараций локальных переменных и списка операторов. Для каждого блочного оператора порождается новый контекст, в котором регистрируются локальные переменные. Контекст объемлющего блока становится его родителем. Далее происходит анализ последовательности операторов блочного оператора на основе нового контекста. Входные и выходные параметры блока определяются как объединение входных и выходных параметров всех внутренних операторов. После проведения операции объединения контекстов внутренних операторов для описания внешних зависимостей из построенного объединённого контекста удаляются упоминания о локальных переменных блочного оператора. Результат такого просеивания будет входом/выходом для блочного оператора вцелом. В дальнейшем при анализе зависимостей в родительском блоке по отношению к переменным внутреннего блока будет использоваться только построенный таким образом контекст.
Зависимости для внешних переменных, использующих внутренние переменные блока, строятся следующим образом. Скалярные переменные и массивы сначала исключаются из списков входных и выходных зависимостей, затем анализируются индексы, и если они содержат вхождения локальных переменных (не важно, массивов или скаляров), то индексы заменяются на диапазон, описывающий длину соответствующего этому индексу измерения. Если элементы массива из диапазона входят в условные операторы, то такие диапазоны помечаются. Так поступают, поскольку невозможно гарантировать изменение всех элементов массива, соответствующих данному диапазону, и нельзя указать точно, какой элемент меняется.
Далее обратимся к методу анализа зависимостей в циклах. В виду сложности анализа производится только анализ цикла for при наложении на него следующих условий:
-
границы цикла должны быть заданы константными выражениями
-
индексные переменные должны меняться только в заголовке цикла строго с шагом единица и не должны меняться внутри тела цикла
-
Внутри тела цикла не должно быть операторов break/continue/return
Первое условие связано со сложностью анализа преобразований переменных вообще. Второе и третье условия гарантируют, что индекс пробежит все значения из диапазона определённого границами цикла. Игнорирование этих требований может привести к некорректному результату. Например, какой-то элемент массива из диапазона может остаться неинициализированным, но будет помечен как получивший новое значение. Последующие операторы будут думать, что значение этого элемента они должны получить от этого цикла, но в действительности они получат «мусор», а не то значение, какое бы получили при последовательном исполнении. Логика исходной программы будет нарушена. При этом требование единичного шага итерации цикла не критично и легко может быть снято, в текущей реализации присутствует из соображений простоты реализации.
Анализ зависимостей по данным в цикле разбивается на несколько этапов. На первом этапе для каждой итерации цикла производится анализ зависимостей переменных, встречающихся в теле цикла, от других итераций данного цикла. На следующем этапе производится преобразование зависимостей для тела тела цикла в зависимости от внешних по отношению к циклу переменных. Далее определяется выход цикла, то есть та часть данных, которая была изменена во время исполнения цикла. Далее во всех операторах, где будет использоваться переменные, которые использовались циклом, будут присутствовать в зависимостях только рассматриваемая изменяемая часть цикла. Например для цикла
for(i=1; i<=10; i++)
a[i][i+1] = 1; выход будет a[1][2], a[2][3] … a[10][11], а не a[1][2], a[2][2], a[1][3] …
Анализ условных операторов (if, switch) производится следующим образом. Для построения зависимостей строится объединение In и Out от всех ветвей условного оператора. К сожалению, в статике редко удаётся предсказать, какая именно ветка условного оператора выполнится. Поэтому, затем, при преобразовании зависимостей в граф, весь условный оператор представляется как одна вершина.
Далее, по всем найденным зависимостям строится граф. Просмотр начинается с функции main С-программы, в которой производится проход по всем операторам функции. Если среди операторов встречается вызов функции или цикл, или условный оператор, то по ним принимается решение о том, нужно ли рассматривать данный оператор как единое целое, или можно его разделить на части и каждую часть рассматривать отдельно. Операция такого разбития оператора на составные части в дальнейшем будет называться операцией раскрытия оператора. В результате операции раскрытия вместо одной вершины соответствующей оператору получается группа вершин, состоящая из операторов, входящих в раскрываемый оператор.
Последовательность операторов, которые следуют естественным порядком, тоесть когда операторы выполняются строго последовательно один за другим, без операторов, в которых есть операторы переходов, будем называть линейным участком.
Таким образом, построение графа зависимости производится рекурсивно по всем составным операторам, которые преобразуются либо в одну вершину графа, если оператор не допускает операцию раскрытия, либо в множество вершин, если операция раскрытия допустима. Процесс добавления очередной вершины в граф состоит из определения типа зависимости от других вершин для данной вершины и определения того, какие данные необходимо передать между вершинами в случае наличия между ними зависимости. В случае обнаружения прямой зависимости по данным между двумя вершинами проводится ребро, для которого указываются переменные, участвующие в зависимости и объём пересылаемых данных. Если Out(i) и In(j) пересекаются, то создаётся ребро, направленное от i-ой вершины к j-ой. В случае обнаружения обратной зависимости между 2-мя операторами вершины аналогично соединяются ребром, но поскольку в данном случае важен только порядок следования операторов, а данные не имеют значения, то строится ребро с весом 0. В этом случае ребро направлено таким образом, чтобы не нарушать порядок следования операторов. Тем самым декларируется важность самого факта инициализации передачи данных, а что именно будет передано по ребру не имеет значения.
С целью оптимизации все дуги между парой вершин, независимо от их типа, объединяются в одну дугу с конкатенацией данных. Такой подход позволяет передавать требуемые данные в за одну операцию передачи данных, позволяя тем самым снизить расход времени связанный с латентностью коммуникационной среды.
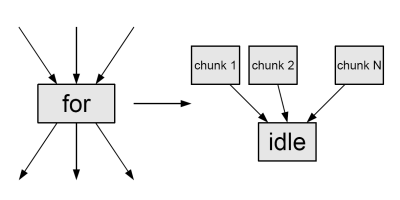
На начальном этапе производится раскрытие всех составных операторов до состояния, когда получаются либо атомарные, либо нераскрываемые операторы. Раскрытие различных составных операторов производится по-разному. Блочный оператор раскрывается всегда. Раскрытие цикла происходит только в том случае, если удается определить границы изменения итератора и в теле отсутствует передача управления (return/break/continue). При выполнении этих условий цикл преобразуется в последовательность итераций, где для каждой итерации явно прописывается значение индекса цикла. Иллюстрацией к раскрытию итераций цикла for является пример, приведённый на рисунке. К сожалению, в текущей реализации нет возможности раскрытия циклов while и do while, главным образом из-за сложности определения границ цикла и отсутствия итератора цикла. Не производится разделение на ветки операторов switch и if else.
Применительно к вложенным циклам можно сказать, что после раскрытия всех итераций получается огромное количество вершин, так, для простого алгоритма перемножения матриц (3 вложенных цикла) и матрицы 10х10 получается порядка 1100 вершин.
for (i = 0; i < 10; i++)
for (j = 0; j < 10; j++)
for (k = 0; k < 10; k++)
Result[i][j] += Left [i][k] + Right [k][j]; В приведённом примере видно, что раскрытие только верхнего цикла дает максимальную степень параллельности 10, тогда как раскрытие еще 2-го цикла увеличивает эту цифру в 10 раз. При таком подходе, т.е. раскрытии всех итераций необходима дополнительная процедура «свертки» графа в соответствии с реальным числом процессоров и минимизацией пересылок, что, к сожалению, в текущий момент не реализовано.
Рассмотрим способ построения фрагмента графа для линейного участка. Пусть S1, S2, …, Si, …, SN — последовательность операторов линейного участка. Между двумя операторами Si и Sj, i<j имеется зависимость во всех случаях, если результаты исполнения i-го оператора нужны j-ому оператору. В данной ситуации, казалось бы, два данных оператора необходимо соединить ребром, однако, если между этими операторами присутствует оператор Sk, который модифицирует переменную, которая требуется на вход j-ому оператору, то будет проведено не одно ребро, а 2 ребра между вершинами, соответствующими операторам Si, Sk и Sk, Sj.
Процесс построения начинается от последнего оператора и продолжается в обратную сторону. Для оператора, у которого переменная var ∈ In(i) входит во множество входов оператора, ищется ближайший к нему оператор, у которого данная переменная входит во множество выходов оператора var ∈ Out(i). Весом ребра становится количество байт, занимаемое переменной, участвующей в зависимости. Так продолжается до тех пор, пока не будет достигнут первый оператор. В случае, если для пары операторов прямая зависимость не выявлена, ищется обратная зависимость. Вне зависимости от наличия прямой или обратной зависимости для последовательности операторов ищутся зависимости по выходам.
Каждой вершине графа сопоставлен её вес. Как уже говорилось ранее, это число, характеризующее вычислительную сложность вершины. В данном случае это оператор, как атомарный, так и составной (цикл, условный оператор, вызов функции). Данная информация необходима в дальнейшем для алгоритмов планирования вычислений. В данной реализации вес оператора считается как число эталонных операций и в качестве эталонной операции выбрана операция сложения двух чисел с плавающей точкой. Таким образом, для атомарных операций можно произвести очень приблизительный подсчёт их времён исполнения относительно вычисления операции сложения. Для составных операторов всё обстоит несколько сложнее, поскольку они состоят из множества операторов. Среди множества операторов могут встречаться вызовы функций, о времени вычисления которых на этапе статического анализа программы может не оказаться сведений.
Для условных операторов вес вычисляется как сумма весов условия оператора и максимального значения веса одной из альтернатив. Вес линейного участка кода вычисляется как сумма весов составляющих его операторов.
Обратимся к вычислению весов циклов. Для определения веса цикла for необходимо знать численные значения границ изменений параметра цикла и вес его тела. Для нескольких вложенных операторов for:
for (I 1 = L 1; I 1 <= U 1; I 1++) { … for (I 2 = L(I 1); I 2 <= U(I 1); I 2++) { … for (I K = L(I 1, I 2, …, I K–1); I K <= U(I 1, I 2, …, I K–1); I K++) { Body(I1, I2, …, IK) } … } … } вес будет вычисляться по формуле:
| Weight = |
U1 |
(… + |
U2(I1) |
(… + |
Uk(I1, I2, …, Ik–1) |
BodyWeight(I1, I2, …, Ik) + …) + …) |
| Σ |
Σ |
Σ |
| I1=L1 |
I2=L2(I1) |
Ik=Lk(I1, I2, …, Ik–1) |
где тело и диапазоны изменения границ вложенного цикла зависят от параметров объемлющих циклов. Как видно из приведённой формулы, большая степень вложенности влечёт большие вычислительные затраты при вычислении веса.
К сожалению, про число итераций цикла while как правило ничего сказать нельзя, поэтому вес цикла считается как вес его тела. Тоже самое относится и к циклу do while.
|
|


 Общее описание
Общее описание